Анализ вариабельности сердечного ритма при аритмиях с сохраненным синусовым ритмом
А.В. Мартыненко,
Н.И. Яблучанский
Факультет фундаментальной медицины
Харьковского национального университета им. В.Н. Каразина
Постановка проблемы
Технология вариабельности сердечного ритма (ВСР) из разряда
теоретических в последние годы перешла в практические и все шире используется в самых разных разделах медицины [4, 5].
При этом на практические приложения технологии ВСР накладываются серьезные ограничения, а именно, приложением к сердечным интервалам с сохраненным синусовым ритмом и частотой экстрасистол не более 3 за 1 мин. [6].
Известно, что не только при патологических, но и в условиях физиологической нормы, синусовый ритм в чистом виде больше правило, чем исключе-ние [1, 2]. По данным суточного мониторирования электрокардиограммы (ЭКГ) у здоровых
наджелудочковые и желудочковые экстрасистолы находят у каждого второго, а в пожилом и старческом возрасте частота их обнаруже-ния увеличивается до 100%. С возрастом возрастает также частота сложных желудочковых аритмий, которая в общей популяции составляет 10-15% слу-чаев. Кратковременные, до 5
комплексов, наджелудочковые тахикардии при АЭКГ наблюдаются у каждого пятого. Если более 5, только у каждого два-дцатого. При ЧСС до 120 уд/мин приступы остаются незамеченными или, по крайней мере, легко переносятся. Кратковременные желудочковой тахикар-дии с частотой до 180 уд/мин в 5% случаях
можно встретить во всех возрас-тных группах.
Все изложенное требует разработки методов, расширяющих границы прило-жений технологии ВСР с ее распространением на аритмии при сохраненном синусовом ритме. В настоящей статье решена данная задача.
Теория
Формально проблема разделения исходной ритмограммы (временного ряда) ЭКГ на кластеры легко решается современными методами кластерного ана-лиза. В наибольшей степени для последующего анализа подходит метод К-средних, где для наперед заданного числа кластеров К отыскивается такое распределение членов кластеров, которое минимизирует вариабельность внутри кластера и
максимизирует вариабельность между кластерами. Сте-пень кластеризации характеризуется величиной F. Однако, проблема состоит в том, что анализ величины F при различном количестве заданных кластеров не позволяет установить количество независимых источников, формирую-щих исходную ритмограмму. Для
выделения независимых источников ис-пользуется предлагаемый в статье алгоритм, позволяющий найти решение указанной проблемы не во временной, а в спектральной области.
Центральная теорема спектрального анализа, связывающая интеграл от квадрата
функции с мощностью спектра (ТР) ВСР, была открыта А.М.Ляпуновым в 1896 г. и впервые опубликована в Известиях математического общества Харьковского университета. Дискретный аналог указанной теоремы для N значений функции fN при сохранении первых М гармоник имеет вид [3]:
где, Am, Bm – коэффициенты Фурье функции fN; ?(М) – ошибка разложения функции.
Представляя исходную функцию К кластерами перепишем (1) в виде:
где, am, bm – коэффициенты Фурье для каждого из К кластеров, объединение которых представляет функции fN; ?k(М) – ошибка разложения для k-ого кла-стера.
Тогда минимум функционала
будет решающим правилом для выделения К независимых источников в исходной ритмограмме, т.к. минимальная ошибка ?(М) реализуется только при собственном разложении гармонического сигнала и максимизируется при произвольном объединении сигналов от гармонических источников.
Модельная задача
Проиллюстрируем изложенный метод на простейших примерах:
объедине-ние 2-х и 3-х гармонических сигналов.
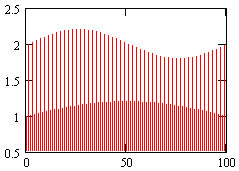
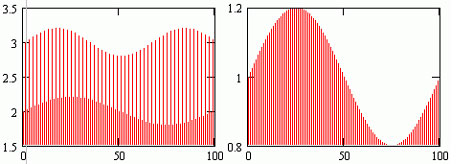
Объединение двух сигналов представляет собой перемежающийся сигнал от 2-х разночастотных гармонических источников (рис.1): 1+0.2sin(10?t) и 2+0.2sin(20?t).
Рис.1
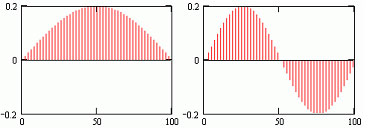
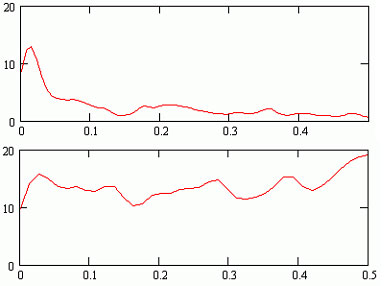
Разделение на 2 независимых сигнала показано на рис.2. Спектральное
разложение в этом случае дает минимальную ошибку ?=0.2% и соответствует точному представлению независимых источников.
Рис.2.(а,б)
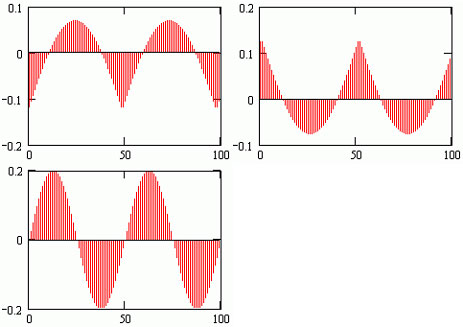
Попытка разделение исходного сигнала (рис.1) на 3 независимых источника представляет комбинацию действительных сигналов, формирующих исходный, и дает ошибку ?=22.8%, т.е. максимизирует ее.
Рис.3 (а,б,в)
Легко видеть, что разделение объединения 2-х независимых источников производится достоверно и точно.
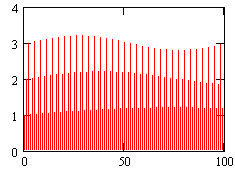
Объединение трех сигналов представляет собой комбинацию сигналов от 3-х
разночастотных гармонических источников, полученную с помощью их по-следовательной циклической перестановки (рис.4): 1+0.2sin(10?t), 2+0.2sin(20?t) и 3+0.2sin(30?t).
Рис.4
Попытка разделения на 2 независимых сигнала показана на рис.5. Ошибка
спектрального разложения в этом случае максимальна ?=22.3%, т.к. в разло-жении получена комбинация сигналов от независимых источников.
Рис.5.(а,б)
Разделение исходного сигнала (рис.4) на 3 независимых источника позволяет точно определить истинные составляющие и минимизирует ошибку ?=0.2%. Разделение на кластеры и в этом случае выполняется абсолютно точно.
Попытка разделения на 4 независимых сигнала снова максимизирует ошибку
спектрального разложения ?=18.6%, т.к. в разложении получена комбинация сигналов от независимых источников.
Видим, что разделение объединения 3-х независимых источников также производится достоверно и точно.
Реальная задача
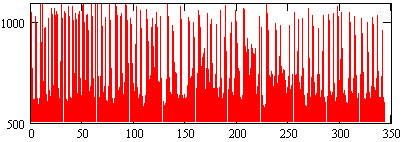
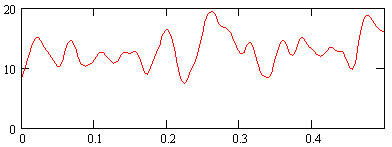
Рассмотрим случай юношеской аритмии: 5-минутная запись здорового мальчика 12 лет (рис.6).
Рис.6
Последовательное разделение исходного сигнала (рис.6) на 2-5 кластеров дает следующие ошибки разложения: 2 кластера – ?=2.9%; 3 кластера – ?=1.7%; 4 кластера – ?=1.0%; 5 кластеров – ?=18.2%. В соответствии с этим можно
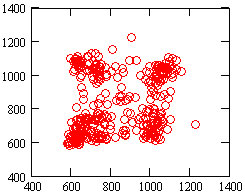
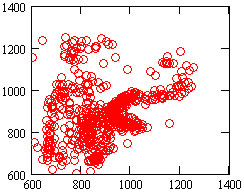
утверждать, что мы наблюдаем 4 независимых источника, форми-рующих ритмограмму (рис.6). Анализ скатерограммы этой записи подтверждает вывод (рис.7).
Рис.7
Интересно проанализировать характер сигналов, формирующих ритмограмму ЭКГ.
Для этого рассмотрим спектры независимых источников. Например, при разделении ритмограммы на 2 независимых источника, их спектры выглядят сильно зашумленными случайной компонентой ВСР (рис.8).
Рис.8.
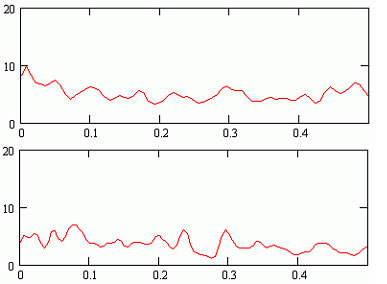
Тоже в случае разделения на 3 и 5 сигналов. Только при выделении 4 независимых сигналов удается идентифицировать 1 гармонический источник и 3 стохастические компоненты формирующие ритмограмму ЭКГ. На рис.9 представлены
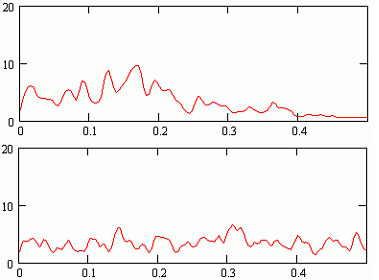
спектры 1 гармонического источника (синусового узла) и суммарный спектр от 3-х стохастических компонент.
Рис.9
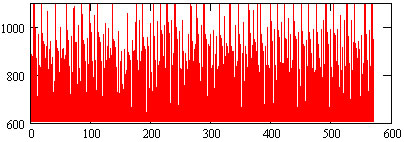
На рис.10 для сравнения показан спектр от стохастического источника
с нормальным законом распределения.
Рис.10
Благодаря указанным разложениям может быть корректно подсчитана и
общая мощность спектра для ритмограммы рис.6: ТР было уменьшено от 15290 мс2 для спектра исходной ритмограммы до 4930 мс2 при делении на 4 независимых источника. Последнее значение ТР гораздо ближе к среднему значением
ТР для данной возрастной категории.
Аритмия. Пациентка Л. 60 лет, аритмия. Ритмограмма дана на рис.12.
Рис.12
Анализ скатерограммы (рис.13) не позволяет выявить количество независи-мых источников.
Рис.13
Последовательное разделение исходного сигнала (рис.12) на 2-4 кластеров дает следующие ошибки разложения: 2 кластера – ?=2.2%; 3 кластера – ?=16.0%; 4 кластера – ?=21.1%. Можно утверждать, что мы
наблюдаем 2 не-зависимых источника, формирующих ритмограмму ЭКГ (рис.12). Спектры при 2-х сигнальном делении свидетельствуют о наличии одного гармонического и одного стохастического источников (рис.14).
Рис.14
Подсчет ТР при двухсигнальном разложении позволяет существенно
скор-ректировать его значение от 14750 мс2 в первоначальном варианте до 2020 мс2 при двухсигнальном разложении.
Выводы
Предложен математический метод, позволяющий использовать спектральные методы ВСР для анализа записей с аритмиями.
В статье показано, что:
- предложенный метод точно и достоверно разделяет смешанную модельную запись на независимые источники;
- при разделении на независимые источники реальных записей ВСР
удается выделить гармонические и стохастические независимые источники, что под-тверждает точность процедуры и адекватность ее результатов физиологиче-ским представлениям о природе ВСР;
- вычисленные для разделенных источников величины общей мощности хорошо коррелируют
с ожидаемыми величинами ТР ВСР для данных возрас-тных групп;
- дополнительного исследования требует вопрос о целесообразности вклю-чения стохастической компоненты спектра в оценку ТР ВСР.
Так как в анализе ВСР рассматривается регуляторное воздействие на источ-ник гармонического
сигнала – синусовый узел, можно попытаться ограни-читься только гармонической частью спектра. Тогда ТР ВСР в первом случае будет 2550 мс2, а во втором – 1400 мс2, что хорошо совпадает со средними значениями этого показателя для указанных возрастных категорий.
Разработанный метод может быть использован и для корректной оценки ТР ВСР и детального
анализа спектральных характеристик синусового узла при аритмиях.
Литература
- Добове моніторування ЕКГ. Рекомендації українського товариства кардіології,
Київ, 2002, 76 с.
- Яблучанский Н.И., Мартыненко А.В., Исаева А.С. Исследуем регулятор-ные процессы. Для настоящих врачей, Харьков: 2005, 156 с.
- Хемминг Р.В. Численные методы. М.: Наука, 1972, 400 с.
- Aubert AE, Ramaekers D. Neurocardiology: the benefits of irregularity. The basics of methodology, physiology and current clinical applications. Acta cardiol 1999; 5(3): 107-120.
- Baevskii R.M. Analysis of Heart Rate Variability in Spase Medicine. Human Phisiology. 2002; 28(2), 70-82.
- Task force of the European Society of Cardiology and the North American Soci-ety of Pacing and Electrophysiology. Heart rate variability. Standards of measure-ment, physiolo¬gical interpretation and clinical use. Circulation 1996; 93: 1043-1065.
Medicus Amicus
|








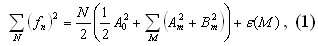
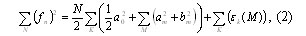
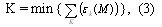

 Новости
Новости 